Maths projects
Modelling clickstream data - Jonathan Cumming
Description
A single visit to a website (or “session”) can be represented as a sequence of webpages visited within that site. This sequence of page visits is known as a clickstream or click path, and analysis of this data is good example of data science which is particularly useful for web activity analytics, advertising and marketing, and improving profit of e-commerce sites. In this project, we will look at some simple statistical methods for modelling clickstream data and will evaluate them on a real problem provided by Clicksco.
We can consider the clickstream for a single session as a sequence of categorical variables \( (X_1, \dots, X_n) \), where \(X_i\) is the \(i\)-th visited page and n is the number of pages visited. The simplest model for a session could then be a Markov chain, where at any time t the user randomly selected a new page, \(X_{t+1}\), and moves to that page according to a probability distribution over the available webpages which depends only on the current page, \(X_t\).

An example Markov chain model.

Visualisation of a Markov chain transition matrix as a site map
The Markov chain allows us to summarise all of the movement through the website via the matrix of transition probabilities \( P[X_{t+1} |X_t]\), which provides a simple mechanism for prediction as well as an effective way to map the traffic through the site. However, the main advantage and chief limitation of the Markov chain is its lack of memory (the next page depends only on the current one), which makes it computationally quick and easy but makes it impossible to use information previous to the current page.
A more sophisticated approach would be to use a Hidden Markov Model (HMM) where we now have an additional "hidden" variable \(Y_i\) at each time point \(i=1,\dots,n\) which can be considered as the background mode of the user’s activity (e.g. "browsing", "updating preferences", "shopping", "just here to pay my bills"). In an HMM, it is this background "hidden state" which evolves like a Markov chain, and now the types of pages visited depend only on the value of this background state (e.g. visiting the Basket will be more likely under a "shopping" state than a "browsing" state).
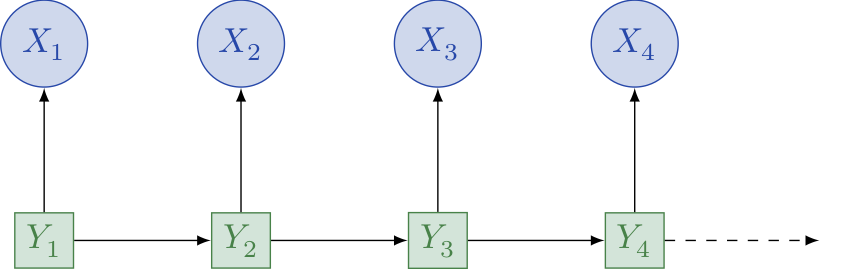
An example Hidden Markov model.
While a more complex model to work with, HMMs could potentially lead to more valuable information and a richer interpretation (it could be useful to know if the user is in ‘shopping’ mode!).
In this project, we study these methods for clickstream analysis, and investigate the methodology of Markov models and HMMs as potentially useful approaches. Beyond this, future directions could include:
- examining Bayesian approaches to HMMs
- investigating key questions in model development (model comparison, how many states, how many hidden states)
- exploring alternative regression modelling approaches to clickstream data
- incorporating covariate information into your models (e.g. time spent on the page).
This project has a focus on statistical methodology and data analysis. Familiarity with the statistical package R, general statistical concepts, and data analysis are essential.
Prerequisites/Corequisites
Statistical Concepts II, Statistical Methods III
Bayesian Statistics III/IV and Topics in Statistics III/IV may be helpful, but are not essential
References
- Rabiner, L.R., 1989. A tutorial on hidden Markov models and selected applications in speech recognition. Proceedings of the IEEE, 77(2), pp.257-286. DOI: Link
- Ghahramani, Z., 2001. An introduction to hidden Markov models and Bayesian networks. International Journal of Pattern Recognition and Artificial Intelligence, 15(01), pp.9-42. DOI: Link
- Montgomery, A. L., et al., 2004. Modeling Online Browsing and Path Analysis Using Clickstream Data. Marketing Science 23(4), pp.579-595. Link
- Scholz, M., 2016. R Package clickstream: Analyzing Clickstream Data with Markov Chains. Journal of Statistical Software, 74(4), 1-17. Link