Other remarks

1. Bases are generally deleted by using the XBASE:  command discussed below. However, whenever a base becomes redundant because all its constituents have been deleted using the XELEMENT:  command, the base too is removed.
2. As far as possible we take no account of the ordering in a collection: an element either belongs to a base, or not, and we prefer to regard its position in the base as not of interest. (The important exception is for the input of belief matrices using the VAR:  command.) However, it is possible to refer to the 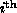member of a base according to the ordering convention using the notation [<B:I>], where B is the name of the base, and I is an integer. The effect of this notation is as follows. Every line input to [B/D] is parsed before any action is taken. A quantity of the form [<B:I>] is replaced by the name of the element or data carrier having position I in the base B. You should beware using this facility as it depends crucially upon the ordering convention (this is discussed in the glossary), and this will - of course - change as elements and data carriers are introduced and deleted.
3. Two operators are available to count the number of bases and elements in bases. The count  operator counts the number of elements, but not bases or data carriers, in a base. The countb  operator counts the number of either elements or bases, but not data carriers, in a base. The countd  operator counts only data-carriers, and excludes elements possessing data. The countany  operator counts all constituents of a base, i.e. data-carriers, elements, and other bases.
4. It is possible to define bases of bases. In particular, a base of bases can be used during adjustments. See §9.1.2 for further details.