It is necessary to specify prior beliefs over the four quantities
, and for the error components. Noninformative reference
prior distributions are used for all these quantities by
[1]. As we are concerned only with developing the example
insofar as it illustrates the construction of influence diagrams, we
provide here fictitious but credible prior beliefs about these
quantities. In doing so, we have attempted to portray degrees of
uncertainty that might plausibly be held by the process production
manager. (For genuine solvable problems, we should be able at
least to elicit prior information for the first and second order
structure.) For the error quantities, we specify 
,
, and 
, so that the the
correlation between the two error components for any given run is about
0.5. (We chose these error variances by examining the
residuals from separate least squares fits, so that the analysis would
not be complicated by obvious conflicts between prior beliefs and the
data.) We specify the following
expectations and covariances between the regression parameters:
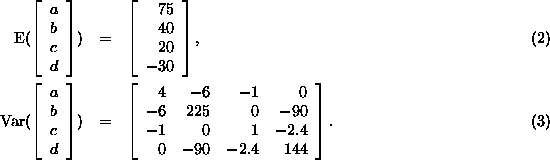
The variance-covariance specifications indicate somewhat more uncertainty about the first regression equation than the second. Each slope quantity is considerably more uncertain than the corresponding intercept quantity: a production manager may know roughly the yield for an average temperature, but may have only sketchy beliefs concerning the direction and magnitude of the slope. We have specified the same degree of weak negative correlation, -0.3, between slope and intercept for each regression.
If we suppose that, at any given temperature, the total
amount of product yield ( 
) will fluctuate between fairly narrow
limits, then the two yields should be strongly negatively
correlated. We choose to introduce this information into the model by
specifying negative correlations (each -0.5) between the two intercepts
and between the two slopes. We treat the slope and intercept for
different regressions as being uncorrelated, as we have exhausted our
intuition about the physical process. This completes the prior
specification process.