For a general belief adjustment we can construct a series of linear
combinations, or canonical directions, with the properties that
the first canonical direction is the linear combination of 
's
with the largest possible resolution; the second canonical direction is
the linear combination with the largest resolution amongst those
combinations which are uncorrelated with the first direction; and so
forth. We take each canonical direction to have prior expectation zero
and prior variance unity by convention. Our term for this collection of
canonical directions is belief grid, as they comprise a
multidimensional grid of directions over which the implications of the
adjustment for the belief structure 
may be summarised as follows.
Each quantity in can be written as a linear combination of the
canonical directions, and the resolution of each such quantity can be
decomposed into a weighted sum of the resolutions for the canonical
directions. The weights correspond to the strength of (squared)
correlation between the quantity and the canonical directions. In this
way, we expect to learn most about those quantities that are strongly
correlated with the first few canonical directions; and least about
those quantities that are weakly correlated with the first few canonical
directions, and strongly correlated with the last few directions.
The belief grid for our simple example consists of the following two canonical directions:
or, in standardised form,
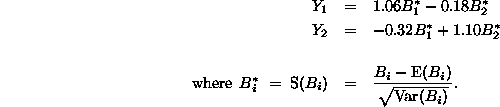
with approximate resolutions
Thus, the linear combination of quantities in 
about which we
expect to learn most is 
, and we expect to remove about 32%
of our uncertainty in this direction. Any other linear combination of
elements in which is highly correlated with will
likewise have a similar variance reduction.
There is only one direction in which is orthogonal to :
we expect to learn least about 
. A resolution of only about 2%
suggests that we learn almost nothing about both and linear
combinations highly correlated with .
Thus, for the purpose of learning about 
and 
, the
information contained in 
is essentially one-dimensional: we
reduce uncertainty only in the direction of . Examination of
the standardised form of the first canonical direction above
shows that is the major component, whereas is the
major component of . Hence, we are learning mostly in the
direction of , and learning very little in the direction of
.