


Next: Adjusted variance
Up: Adjusting beliefs by data
Previous: Adjusted expectation
How should we interpret adjusted expectations? There are four
inter-related interpretations that we can offer.
- The simplest interpretation is to view the quantity
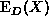 as an
`estimator' of the value of X, which combines the data with simple aspects of
our prior beliefs in an intuitively plausible manner and which leads to a
useful methodology. Alternately, if we have extensive data sources to draw
upon, then we may construct our prior judgements from these sources and use our approach
to develop `estimators' which can be viewed as complementary to certain
standard estimators in multivariate analysis.
as an
`estimator' of the value of X, which combines the data with simple aspects of
our prior beliefs in an intuitively plausible manner and which leads to a
useful methodology. Alternately, if we have extensive data sources to draw
upon, then we may construct our prior judgements from these sources and use our approach
to develop `estimators' which can be viewed as complementary to certain
standard estimators in multivariate analysis. - The second interpretation is to view adjusted expectation simply as a
primitive which quantifies certain aspects of our beliefs, in a similar manner
to the original expectation statement. Indeed, in de Finetti's formal
development of prevision, the principle operational definition that he offers
is that our prevision for X is the value x which we would choose if we were
forced to suffer a penalty

where k is a constant defining the units of loss. In this view adjusted
expectation simply expresses the extension of our choice of preferences from
the certain choice x to the random choice

In the special case where the elements 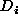 are the indicator functions
for a partition, then this is equivalent to de Finetti's choice for the
operational definition of the conditional prevision,
are the indicator functions
for a partition, then this is equivalent to de Finetti's choice for the
operational definition of the conditional prevision, 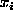 , of X given each
event
, of X given each
event 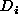 . Under this view, adjusted expectations are simply informative
summaries, generalising the corresponding conditional expectations defined over
indicator functions.
. Under this view, adjusted expectations are simply informative
summaries, generalising the corresponding conditional expectations defined over
indicator functions.
- If we are committed in principle to a full Bayes view based on complete
probabilistic specification of all uncertainties, then we may view adjusted
expectations as offering simple tractable approximations to a full Bayes
analysis for complicated problems. In addition, the various interpretive
measures and diagnostic tests which we shall develop below offer insights which
are relevant to any full Bayes analysis.
- We have described three alternative views of adjusted expectation, each
of which has merit in certain contexts and reflects the contrasting views that
may be held concerning the revision of beliefs. However, we hold a fourth view,
which, by proceeding directly by foundational arguments, subsumes each of the
above views. This view explains why we should view adjusted expectation as a
primitive, the precise sense in which adjusted expectation may be viewed as an
`estimator', and the general properties which may be claimed for the estimate.
Further, it reverses our third interpretation above by identifying a full Bayes
analysis as a simple special case of the general analysis which we advocate.
Our immediate intention is to describe the practical machinery of our approach.
Therefore, we do not at this point intend to take logical and philosophical
diversions into foundational issues, and we shall develop the formal
relationship between belief adjustment and belief revision elsewhere. Instead,
for now we will move between the first three interpretations that we have
listed above, viewing adjusted expectation as an intuitively plausible
numerical summary statement about our beliefs given the data. There is no
implication that this value will fully express our genuine revised belief
concerning the expectation of X. Rather, we have been explicit as to precisely which aspects of our prior beliefs have been utilised in order to assess the adjusted expectation. As with any other formal analysis that we
might carry out, adjusted expectations offer logical information in
quantitative form which we may use as we deem appropriate to improve our actual
posterior judgements.



Next: Adjusted variance
Up: Adjusting beliefs by data
Previous: Adjusted expectation
David Wooff
Thu Oct 15 11:56:54 BST 1998
![]() are the indicator functions
for a partition, then this is equivalent to de Finetti's choice for the
operational definition of the conditional prevision,
are the indicator functions
for a partition, then this is equivalent to de Finetti's choice for the
operational definition of the conditional prevision, ![]() , of X given each
event
, of X given each
event ![]() . Under this view, adjusted expectations are simply informative
summaries, generalising the corresponding conditional expectations defined over
indicator functions.
. Under this view, adjusted expectations are simply informative
summaries, generalising the corresponding conditional expectations defined over
indicator functions.