Background
During the last four years, spectral theory has been taught (by me) in the second term of the module Functional Analysis and Applications IV but this upcomig academic year the content of the second term will be different (I will be teaching the first term, Alpar Meszaros will teach the second term). So I offer the topic as a 4H project instead.
This is a project in Analysis. Spectral theory of linear operators is the generalisation of the matrix eigenvalue problem to infinite-dimensional spaces. Then the so-called spectrum (the complex points \(\lambda\in\mathbb{C}\) where \(A-\lambda I\) is not bijective) may look different to the finite matrix case where the spectrum consists of discrete points that are eigenvalues. In the infinite-dimensional case, \(A-\lambda I\) may be injective but not surjective, in which case \(\lambda\) is not an eigenvalue but a point in the spectrum.
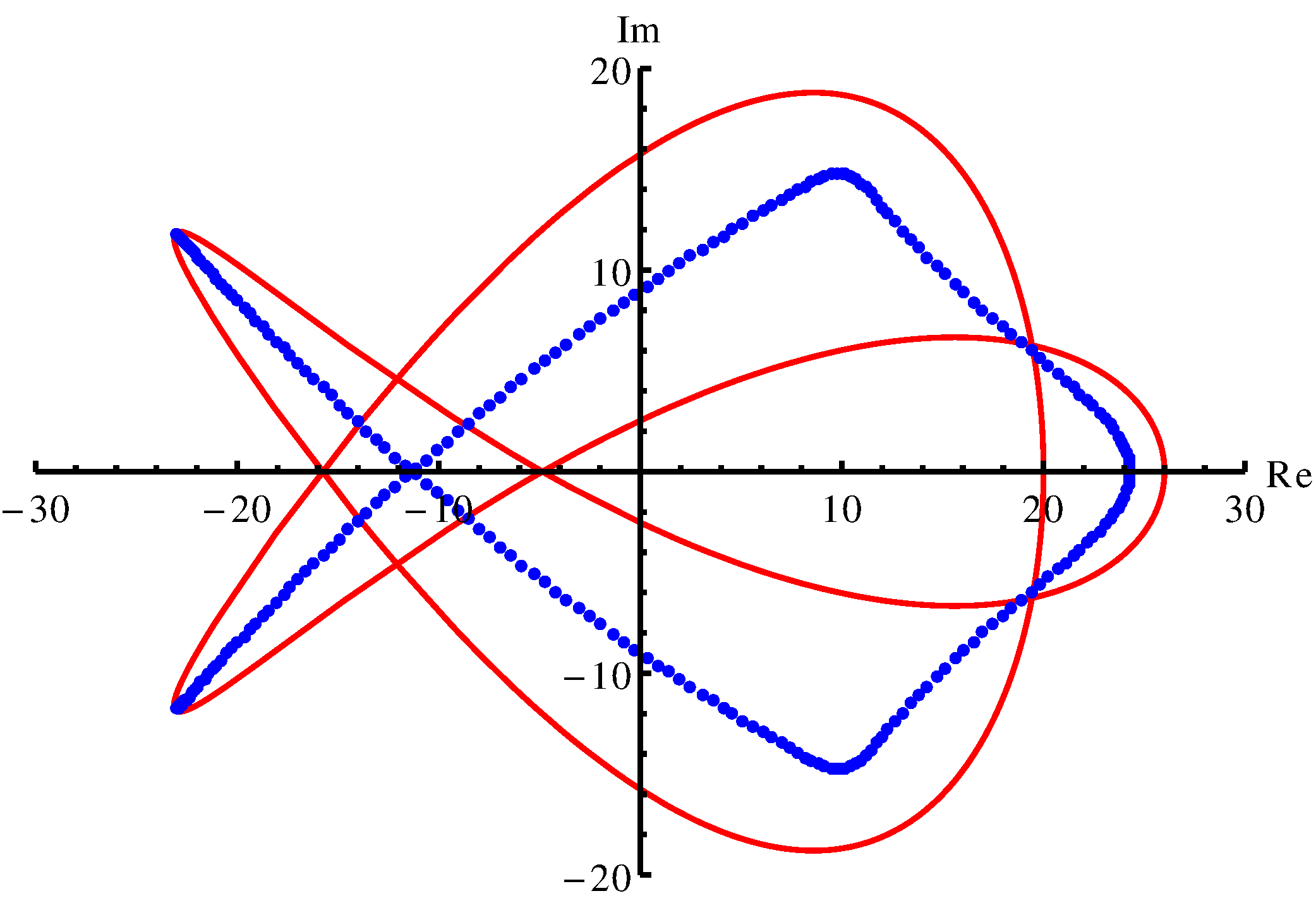 As an example, let's look at an infinite matrix (viewed as a linear operator in \(\ell^2\), the space of square-summable sequences) whose spectrum is given by the red curve in the picture.
This picture is taken from one of my research papers where I studied whether one can approximate infinite matrices by truncating them to finite sections. The blue dots are the eigenvalues of the \(n\times n\) sub-matrix for (large) \(n=250\). As you see, we don't have convergence (but this brings us off-topic). As you see from this example, the spectrum may be a non-discrete set (in fact, there are examples where the spectrum is a set in the complex plane with non-empty interior, e.g. the shift operator discussed in the lecture notes [1] for which the spectrum is the unit disc). So there are many interesting and suprising properties to be studied in this topic.
As an example, let's look at an infinite matrix (viewed as a linear operator in \(\ell^2\), the space of square-summable sequences) whose spectrum is given by the red curve in the picture.
This picture is taken from one of my research papers where I studied whether one can approximate infinite matrices by truncating them to finite sections. The blue dots are the eigenvalues of the \(n\times n\) sub-matrix for (large) \(n=250\). As you see, we don't have convergence (but this brings us off-topic). As you see from this example, the spectrum may be a non-discrete set (in fact, there are examples where the spectrum is a set in the complex plane with non-empty interior, e.g. the shift operator discussed in the lecture notes [1] for which the spectrum is the unit disc). So there are many interesting and suprising properties to be studied in this topic.
The highlight of the lecture notes is the section on spectral theorems. The spectral theorem for compact selfadjoint operators says that a compact, selfadjoint operator can be viewed as an infinite diagonal matrix with respect to an orthonormal basis consisting of eigenvectors. So this is analogous to the spectral theorem for finite matrices.
Description of the project
We will slowly go through Chapter 1 of the lecture notes [1]. There also exist exercise sheets accompanying the notes which will be useful. The first term will be more of a reading seminar, and in the second term you can focus on individual topics and read material beyond the lecture notes (I will help you find material). Full disclosure: Officially I will be on research leave in the second term and I will be in Cambridge for the first 5 weeks of term - but I will be available to meet online during that time (and I will be back in Durham in time for poster/presentation week).
Prerequisites
Analysis III. It is recommended to take Functional Analysis and Applications IV at the same time as the project as in the first term you learn about bounded and closed linear operators.
References
[1] https://www.maths.dur.ac.uk/users/sabine.boegli/FAA4_Epiphany.html