Description
The aim of this project is to understand the main features of the classification of finite dimensional simple Lie algebras over the complex numbers. Simple Lie algebras are of fundamental importance in group theory, representation theory, number theory and mathematical physics, but to begin to understand them we only need a bit of (mainly linear) algebra.
The main idea in the classification is to associate a 'root system' to each simple Lie algebra; this is a finite set of vectors in a real vector space with many nice geometric properties (for example, it is invariant under certain reflections). Here are pictures of two of the simplest root systems. The one on the left is called $A_2$ and the one on the right is called $G_2$. They are each generated by two vectors $\alpha$ and $\beta$:
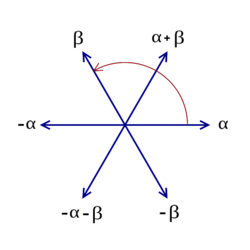
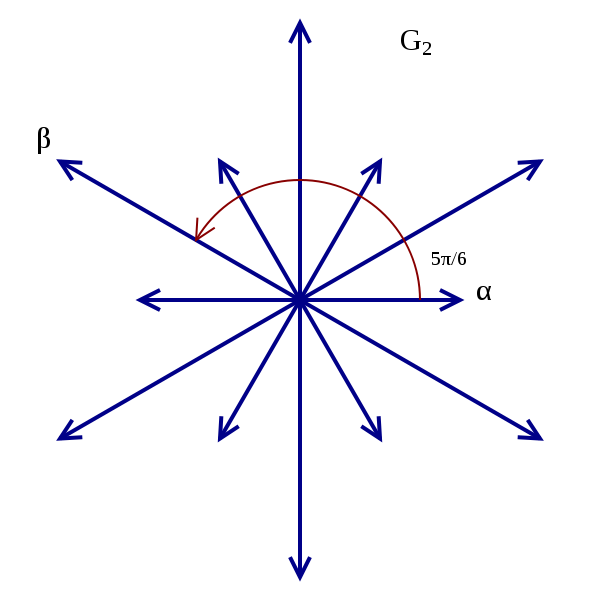
We will then look at root systems of simple Lie algebras (which are "irreducible" root systems), study some of their properties, and try to understand some of the ingredients leading to their classification via a special type of graphs called Dynkin diagrams. The irreducible root systems are classified into four infinite series $$A_n,B_n,C_n,D_n$$
together with five "exceptional" types
$$E_6,E_7,E_8, F_4, G_2.$$
These correspond to the Dynkin diagrams:

Finally, there are several possible further directions to investigate individually: Lie groups, Finite simple groups, linear algebraic groups, Witten zeta functions, etc.
Prerequisites
Algebra IIResources
- R. Carter, G. Segal, I. Macdonald, Lectures on Lie
Groups and Lie Algebras (Carter's chapter is a
very readable introduction and gives a good overview but
without proofs)
- R. Carter, Lie Algebras of Finite and Affine Type
- K. Erdmann and M. Wildon, Introduction to Lie Algebras
- D. M. Tsonev, Simple Lie Algebras and their
Classification, link