Project IV (MATH4072) 2014-15

Cobordisms

D Schuetz

Description

One of the most basic, but also one of the most important classes of spaces in topology is the class of manifolds. These spaces, wich can be thought of as higher dimensional analogues of surfaces, appear in many branches of mathematics, for example, as solutions to algebraic equations or as configuration spaces of mechanical systems. Cobordisms are manifolds with boundary whose boundary splits into two distinguished parts, each forming a manifold.

On the most basic level, a closed interval can be considered a cobordism between a point (a 0-dimensional manifold) and another point, or as a cobordism between two points and the empty set. In one higher dimension, the following picture shows a 2-dimensional cobordism between a circle and two circles.

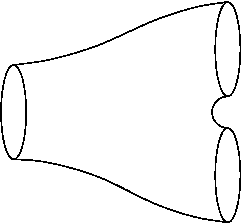
cobordism

This gives rise to a very intriguing equivalence relation on manifolds, which is reasonably simple in low dimensions, but for higher dimensions seems to be impossible to understand. However, seminal work of Rene Thom in the 50's has shown that this concept can be understood quite well and leads to a fascinating subject.

Furthermore, compact manifolds without boundary can be decomposed into a finite sequence of cobordisms, which in turn can be used to understand the structure of the manifold. This approach has led to a proof of the generalised Poincaré Conjecture in high dimensions, via the celebrated h-cobordism Theorem.

Another area where cobordisms appear is in Topological Field Theories. These have originally been invented by physicists, but they have since been applied in various areas in pure mathematics, such as 4-manifolds and knot theory. One of the most important results in mathematics in recent years is the proof of the Cobordism Hypothesis, which gives a form of a classification of certain topological field theories.

Prerequisites

Topology III.

We recommend to take Algebraic Topology IV.

Resources

Information on differentiable manifolds can be found in any book on Differential Topology (see 515.16 in the library), for example Differential Topology by Morris Hirsch. Not every book will explain what a cobordism is (Hirsch does), but for that you can look at the wikipedia page.

More information on cobordisms is also in Lectures on the h-cobordism theorem by John Milnor.

An introduction to the cobordism hypothesis is given in the article by Daniel Freed, Bull. AMS 50 (2013), 57-92.

email: D Schuetz

Back