Rank-driven processes
These are systems of a fixed number of particles in space which are updated by the removal of one or more particles according to a criterion based on some ranking of the particles based on their locations, with removed particles being replaced by new random entrants to the system.
With Michael Grinfeld and Philip Knight, we looked at processes of particles in $[0,1]$, with the criterion for removal based on linear order: for example, remove the smallest particle and two other particles selected randomly according to their rank. This sort of model was inspired by the Bak–Sneppen model of evolution, which is a more complicated model that also involves some graph geometry. Under suitable conditions, for many particles and long times, the empirical distribution of particles in the system converges to the uniform distribution on $[s^*,1]$, where the threshold $s^*$ is determined by the distribution for replacement.
A related model takes place in $[0,1]^d$, and removes particles that are extreme with respect to the distance from the centre of mass of the particle cloud. With Michael Grinfeld and Stas Volkov, we looked at convergence of this model.
Click on the buttons below for some of my work related to convex hulls of random walks.
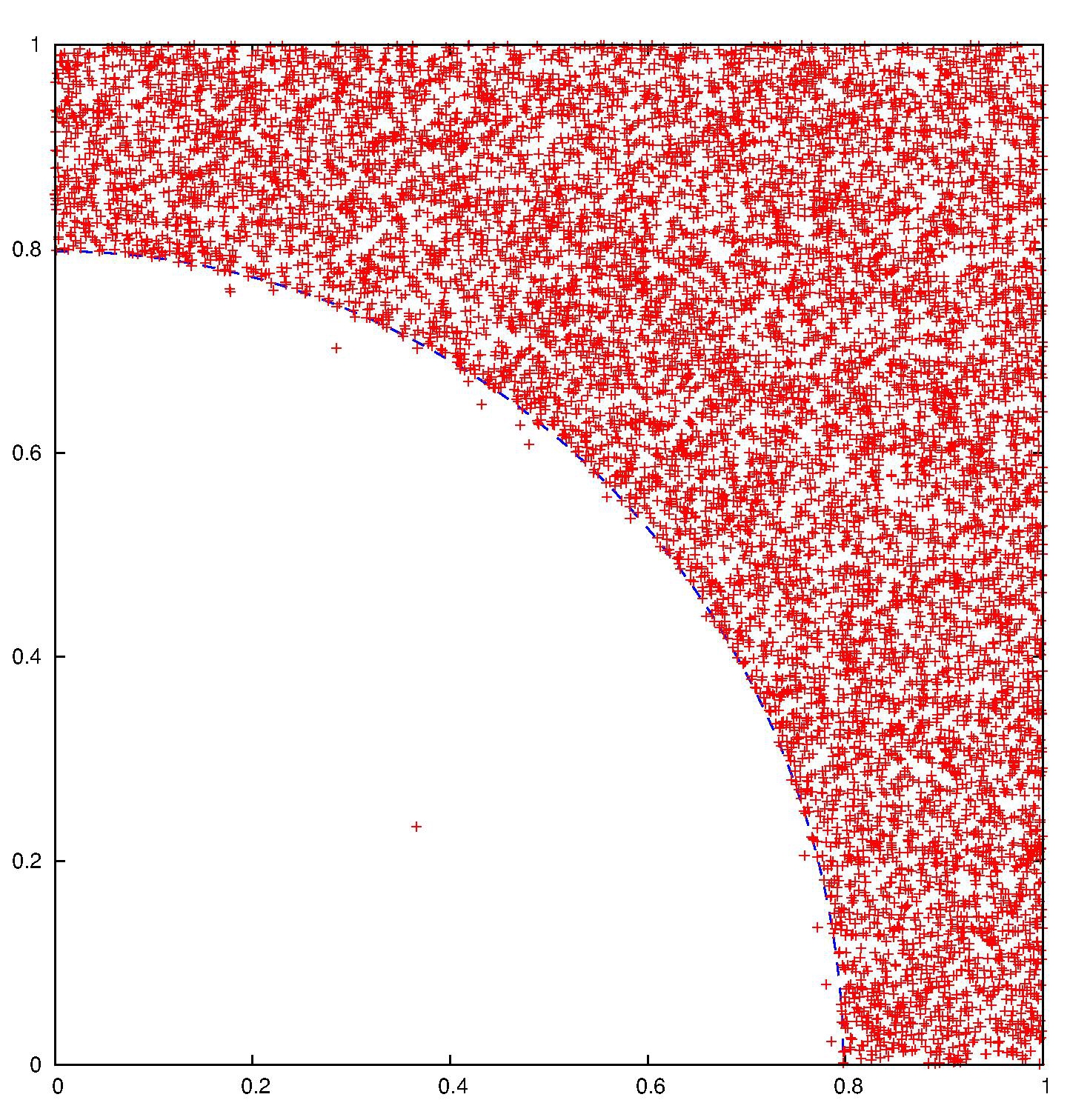
Here's a system of points in the square which evolves by the removal of two particles at each step, the one closest to the origin, and one other uniformly at random. They are replaced by two uniform points on the square. The limit shape of the bulk of the cloud is the complement in the square of the quarter-disc centred at the origin with radius $\sqrt{2/\pi}$.
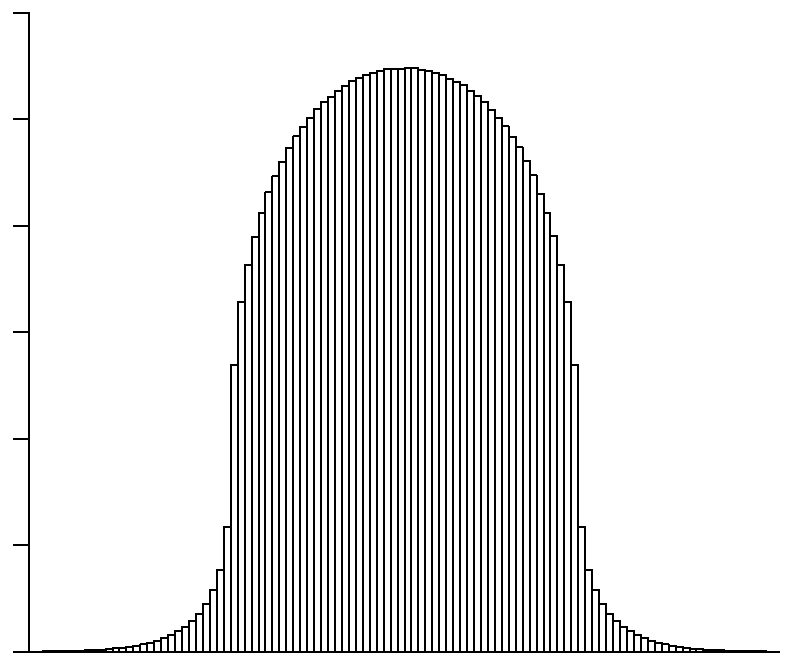
The distribution for the limit point of the barycentric elimination model on $[0,1]$ that starts from an initial configuration of many independent uniform random points.