Convex hulls of random walks
There are various ways to try to describe the geometry of random walk trajectories in $d$-dimensional Euclidean space. One is to consider the convex hull of the first $n$ steps of the trajectory, that is, the smallest convex set that contains the first $n$ locations of the random walk. What can we say about the convex hull as $n \to \infty$? Its diameter? Its perimeter length or area in the plane, for example, or analogous quantities in higher dimensions?
In the case where the random walk has zero drift and finite-variance increments, the trajectory converges to Brownian motion and the scaling limit carries across to the convex hull and many associated functionals. In the case where the random walk has a drift, in the planar case scaling arguments also give distributional asymptotics for the area. The perimeter and diameter need a different approach, and, while the distributional limits arising from scaling arguments are non-Gaussian, it turns out that the perimeter and diamater have a Gaussian limit, after centering and scaling.
The shape of the convex hull is quite different in the two cases. In the case with drift, it converges to a line segment. In the zero-drift case, the shape fluctuates across all possible convex compact sets.
One can also consider convex hulls of stochastic processes on other spaces, such as manifolds.
Click on the buttons below for some of my work related to convex hulls of stochastic processes.
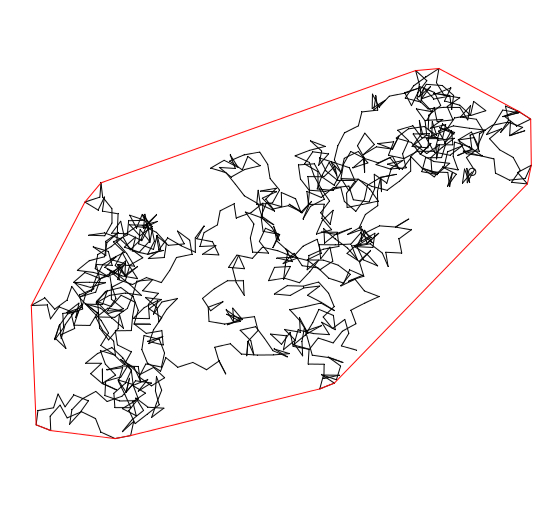
The zero-drift case.
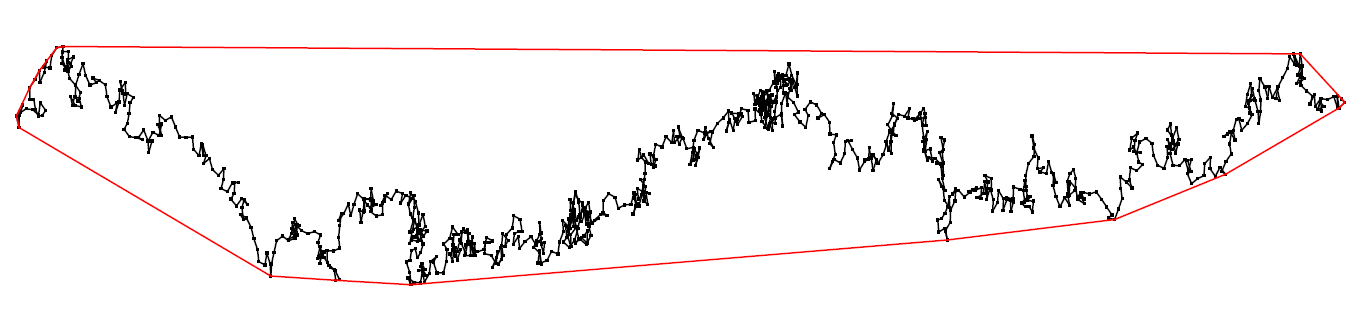
The case with drift.
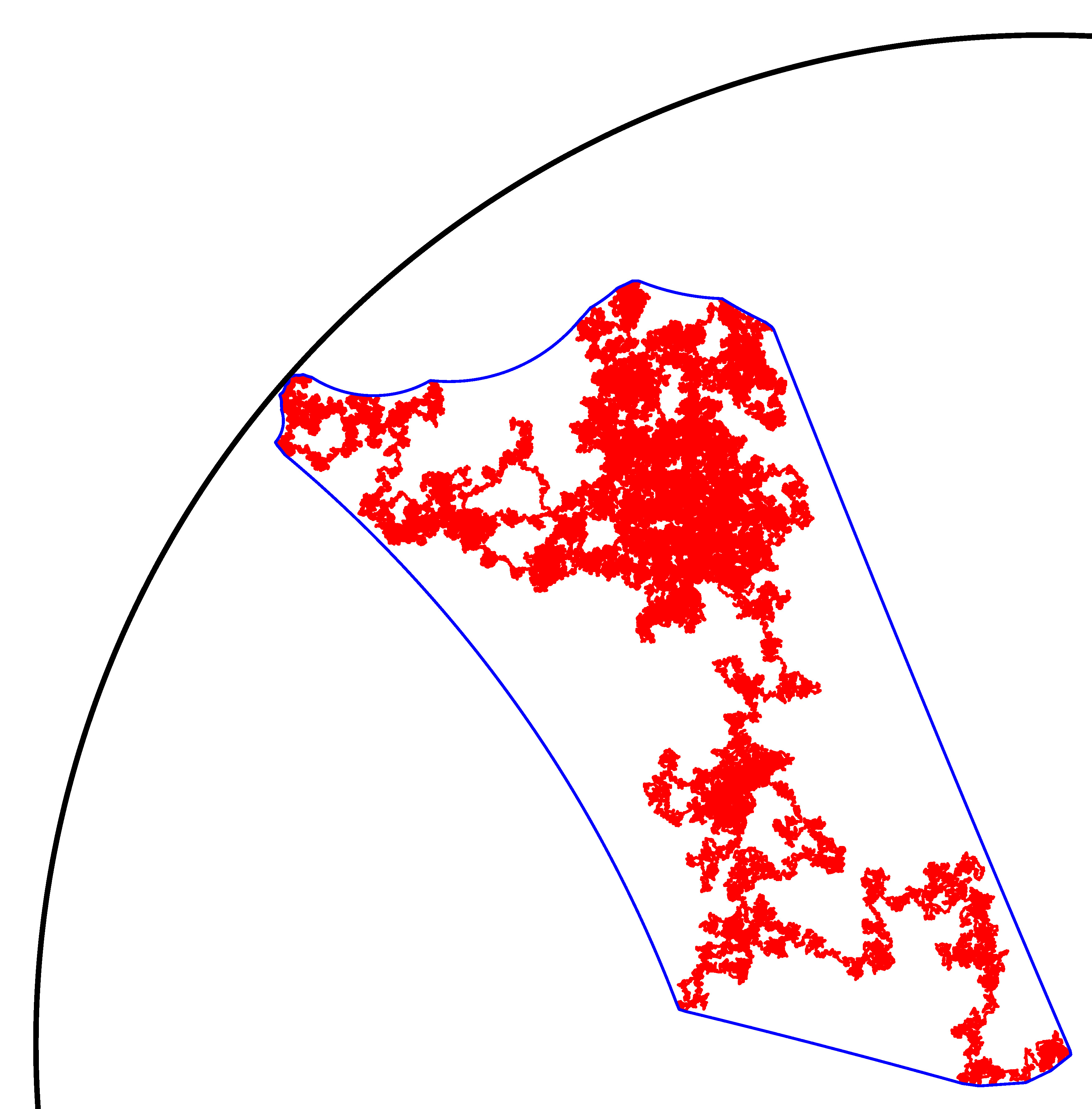
In the hyperbolic disk.